Non-linear mechanics research group
Some of the group lines of research are:
Structural Mechanics, Bifurcation
We develop analytical and numerical methods to understand, analyze and capture structural instabilities. We have paid attention to buckling as well as postbuckling of different instabilities modes such as helical buckling and bulging.
Biomechanics of soft tissue
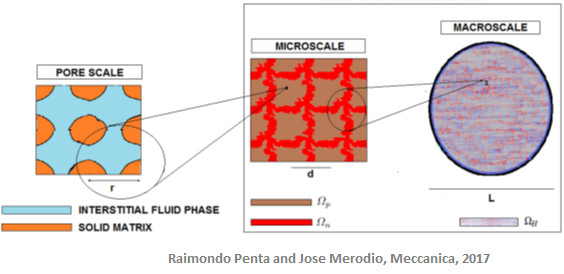
The overall aim of the research is to improve understanding of the (nonlinear) mechanics of biological soft tissue such as arterial wall tissue, with particular reference to the influence of growth, adaptation and residual stress on the mechanical response. We analyze these aspects combining a micromechanical and a macromechanical approach. In our analysis, we incorporate the effects of the microstructure, material properties for the fibers and embedding matrix, as well as the effects of damage (porosity) and residual stresses arising as a consequence of tissue growth.

Cancer Mechanics
A tumor refers to an abnormal growth of cells and can be harmless (no cancer) or dangerous (with cancerous cells). The attempt to give a unified description of what a tumor is from a mathematical viewpoint-as well as from other points of view- is still hopeless because there are too many different types of tumors with different origins and characteristics. Nevertheless, new discoveries relating too many and diverse areas of cancer research make advanced mathematical modeling necessary to elucidate and interpret the experimental findings, as it has just been mentioned previously.
The kinematics (and, in general, mechanics) of large deformations associated with growth is still an open problem. Needless to say that major concern has also been the need to develop constitutive laws (mathematical models of material behaviour), and this remains a key requirement. Such laws are needed in the formulation and solution of boundary-value problems of relevance to clinical procedures and should account for the diverse properties of different tissues. Part of our effort is dedicated to understand these aspects.
Waves
There is a lot of interest in using the equations governing infinitesimal motions superimposed on a finite deformation because it is applicable to several topics. These include: the non-destructive evaluation of prestressed structures before and during loading; the acoustics of soft solids with particular attention to the analysis of biological soft tissues; the (incremental) stability of a free surface of a deformed material, etc. Indeed, surface waves have been studied extensively in seismology, acoustics, geophysics, telecommunications industry and materials science.
